9 aprile 2010

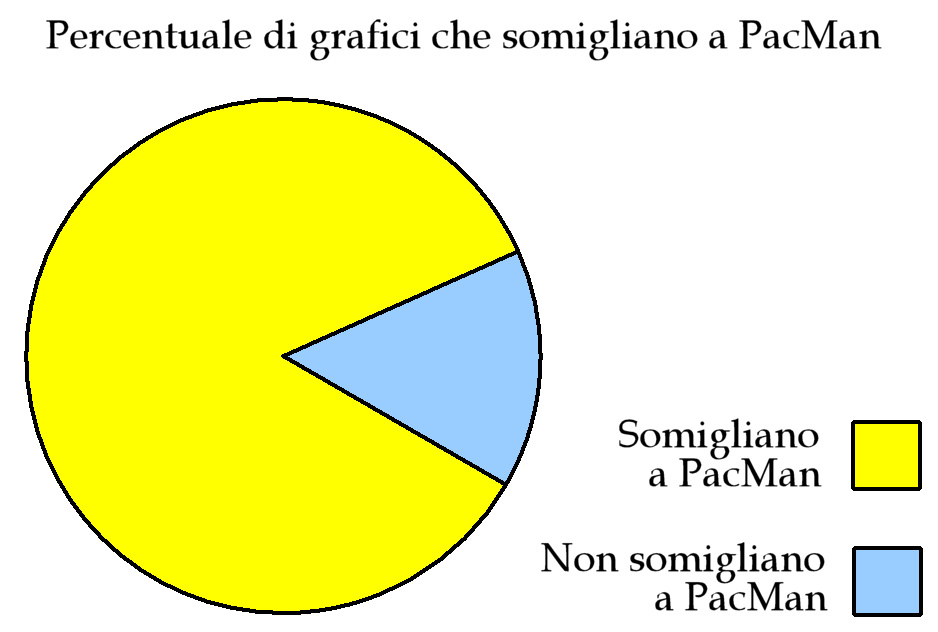
Percentuale di grafici che somigliano a PacMan

Trovata qui e ideata senza dubbio da un genio...

Questo post è stato pubblicato da Mariano Tomatis il 9 aprile 2010

8 aprile 2010

L'arte di Tobia Ravà

Si chiama Tobia Ravà: è un artista italiano di cultura ebraica che ci fa vedere il mondo come solo Neo era in grado di vederlo nella trilogia di Matrix.

Nato a Padova nel 1959, Ravà mescola cabala ebraica, logica matematica e arte contemporanea, nascondendo nei suoi lavori messaggi cifrati che hanno già fatto parlare di "Codice Ravà".

Ho potuto ammirare dal vivo alcune sue opere a Venezia (qui) e mi sono innamorato delle sue Venezie:

Trovo che abbiano un enorme potenziale magico i suoi algoritmi.

Il suo sito è www.tobiarava.com

Questo post è stato pubblicato da Mariano Tomatis il 8 aprile 2010 nella categoria NUMEROLOGIA

31 marzo 2010

Una sorpresa pasquale

Questo esperimento pasquale si basa sul fatto che tu non possiedi poteri di chiaroveggenza: se, infatti, tu fossi in grado di vedere attraverso il cioccolato di un uovo, mi sarebbe impossibile sorprenderti con il suo contenuto.

La mattina di Pasqua, disporrò su un tavolo due uova di cioccolato, A e B. Tu potrai aprirle soltanto da sinistra a destra, prima A e poi B (non potrai aprire prima B).

Una delle due conterrà una sorpresa "inaspettata", l'altra non conterrà alcunché.

L'aggettivo "inaspettata" ha una definizione ben precisa: con ciò, intendo che - se la sorpresa si trova nell'uovo X - prima di aprire l'uovo X non avrai la certezza logica che la sorpresa vi si trovi all'interno. Dove potrò mettere la sorpresa?

Il mio compito non è facile. Non potrò metterla nell'uovo B, perché una volta che avrai aperto A ti sarai accorto che è vuoto, dunque - sapendo che la sorpresa si trova in una delle due uova - avrai la certezza logica che si trova in B e la sorpresa non sarà "inaspettata" come promesso. Sarò dunque obbligato a metterla nell'uovo A, ma anche qui non sarà "inaspettata" perché tu potrai seguire il mio ragionamento di prima e concludere che devo metterla in A, dunque prima di aprire il primo uovo avrai già la certezza logica di trovarvi la sorpresa.

Se ho dimostrato che la sorpresa "inaspettata" non può trovarsi né in A, né in B, le condizioni di partenza che mi sono imposto sono troppo rigide: non sono in grado di mettere la sorpresa in un uovo e pretendere contemporaneamente che sia "inaspettata".

La domanda chiave riguarda l'apertura dell'uovo A: puoi aprirlo senza sapere se vi troverai o meno la sorpresa? No, perché ti è facile dimostrare che una sorpresa in B non sarebbe "inaspettata". Ciò mi avrebbe imposto, a monte, di mettere la sorpresa in A, e tu aprendolo saprai di trovarvi certamente la sorpresa. Ciò che puoi concludere è che la sorpresa non può essere inaspettata, dunque la mia descrizione del gioco è chiaramente fallace: non posso aver messo alcuna sorpresa "inaspettata".

C'è però una possibilità: che io ti abbia mentito o mi sia sbagliato nell'annunciarti le condizioni del gioco. Ciò fa sì che l'uovo con la sorpresa sia davvero inaspettato! Potrei, infatti, aver messo la sorpresa indifferentemente in A o in B, tanto - avendo mentito o essendomi sbagliato - non vale più la condizione dell'inaspettatezza, e un'eventuale sorpresa in A sarebbe in effetti "inaspettata", perché a priori potrebbe esserci o non esserci e non avresti la certezza logica, prima di aprirlo, di trovarla o meno.

In questo caso, però, la sorpresa davvero "inaspettata" sarebbe in contraddizione con l'ipotesi che l'ha resa inaspettata, ovvero col fatto che io mi sia sbagliato o abbia mentito.

Secondo la maggior parte dei logici, il paradosso sorge dalla mancanza di precisione della definizione di sorpresa "inaspettata". Una via d'uscita dal problema che, sinceramente, ho trovato sorprendente e inaspettata.

Questo post è stato pubblicato da Mariano Tomatis il 31 marzo 2010 nella categoria CHIAROVEGGENZA