14 marzo 2010

Ahmadinejad incastrato da un trucco matematico?

Alla fine degli Anni Sessanta, durante la Guerra Fredda tra Stati Uniti e Unione Sovietica, si diffuse la voce secondo cui i russi spendevano milioni di rubli ogni anno per reclutare medium, sensitivi e individui dotati di capacità chiaroveggenti, per destinarli a mansioni di spionaggio e controspionaggio "psichico". Il 25 gennaio 1963 il Time aveva pubblicato un articolo dedicato a Rosa Kuleshova, intitolato "Vedere con la punta delle dita"; l'idea che una ragazza russa di 22 anni potesse leggere da bendata faceva tremare l'intelligence americana: come difendere i propri segreti dalle spie psichiche oltre la Cortina di Ferro? Sarà il matematico Martin Gardner a smascherare i suoi trucchi nel 1981.

Prova che lo spionaggio psichico è tutto un inganno? Dipende dall'accezione del termine "chiaroveggenza". E' nota l'utilità della matematica per scoprire informazioni nascoste, e l'uso che ne ha fatto l'astronomo polacco Boudewijn F. Roukema ha tutta l'aria di un'operazione di raffinato spionaggio. Il 12 giugno 2009 si tengono le elezioni presidenziali iraniane: la sfida è fra Ahmadinejad, presidente uscente e Moussavi, leader dell'opposizione. Il giorno dopo vengono annunciati i risultati. Ahmadinejad ha vinto con il 62,6%. Moussavi, però, denuncia irregolarità nel voto e chiede nuove elezioni. Il 14 giugno 2009 i risultati in dettaglio delle elezioni vengono pubblicati su Internet dal ministro degli interni iraniano; è da qui che Roukema li scarica, con l'idea di tentare una geniale operazione di spionaggio politico: vuole scoprire con la matematica se, a 3000 chilometri di distanza, ci sono state delle irregolarità nel conteggio dei voti. Chiuso nel suo ufficio presso l'Università Nicolò Copernico di Turonia, l'astronomo utilizza per la sua indagine una legge matematica poco conosciuta ma molto potente: la "legge di Benford".

Nel 1938 Frank Benford aveva scoperto che, se si prende una raccolta di numeri tratti dalla vita quotidiana (la popolazione dei comuni di una regione, la quotazione delle azioni di una giornata, i numeri sulle porte di casa di una via), è più facile che un numero cominci con una cifra piccola rispetto al fatto che cominci con una cifra grande; in altre parole, la probabilità che un numero della raccolta inizi con l'uno è circa del 30% mentre la probabilità che inizi con il nove è minore del 5%. Poiché ciò accade soltanto quando i numeri sono scelti da situazioni "naturali", nel 1971 il matematico e consulente di Google Hal Varian ha l'idea di usare la legge di Benford per individuare eventuali falsificazioni nelle raccolte di dati, basandosi sul presupposto per cui chi modifica manualmente delle liste di numeri, difficilmente riesce a farlo rispettando la distribuzione "naturale" delle prime cifre: più probabilmente sceglie i numeri senza pensarci troppo, lasciando quindi le impronte "matematiche" della frode.

Boudewijn F. Roukema utilizza proprio questo metodo(1): città per città, analizza la prima cifra del numero di voti e confronta i suoi conti con quelli "naturali" che seguono la legge di Benford. Su un grafico, tratteggia la linea naturale e fa un pallino per ognuna delle prime cifre: l'1 compare circa il 34% delle volte, quindi lo mette in alto; il 2 compare poco più del 15% delle volte, e così via.

Tutto bene, fino al numero 7: questo compare troppe volte rispetto a quanto ci si aspetterebbe, e il pallino è molto distante dalla linea tratteggiata. E' un campanello d'allarme. Il grafico si riferisce ai voti del terzo candidato, Mehdi Karroubi. Roukema approfondisce la questione, scoprendo che l'anomalia riguarda tre delle sei più grandi aree dell'Iran. In queste stesse zone, il vincitore Ahmadinejad ha una proporzione di voti più alta rispetto alle altre.

E' stata la matematica a condurre lo scienziato polacco dove nessuna spia chiaroveggente è mai arrivata: a supportare statisticamente l'ipotesi di un broglio senza neppure spostarsi dalla propria scrivania!

_________________

⁽¹⁾ L'articolo di Roukema può essere scaricato da qui: http://arxiv.org/abs/0906.2789

Questo post è stato pubblicato da Mariano Tomatis il 14 marzo 2010 nella categoria CHIAROVEGGENZA

14 marzo 2010

Il principio di Kruskal

Nel corso di questo articolo approfondirò un principio statistico ingegnoso e molto utile per la cartomagia, chiamato "Principio di Kruskal" dal nome del suo inventore, Martin David Kruskal (1925-2006).

1) Stendi un mazzo di 52 carte faccia in alto, da sinistra verso destra.

2) Scegli una delle prime dieci carte a sinistra. Il suo valore ti indicherà di quante carte a destra spostarti (se ad esempio hai scelto un tre, dovrai spostarti sulla terza carta successiva. Le figure valgono 1).

3) Il valore della nuova carta ti indicherà di quante carte spostarti di nuovo a destra (se ad esempio sei finito su un asso, dovrai spostarti sulla carta successiva).

4) Prosegui gli spostamenti, che verranno indicati ogni volta dal valore della carta scelta, finché arrivi al fondo del mazzo e dalla carta cui sei arrivato non puoi più spostarti senza oltrepassare l'ultima.

Seppure sembri impossibile, il prestigiatore è in grado di prevedere quale sarà la carta finale!

Ciò è reso possibile da un principio statistico ingegnoso e poco noto, chiamato "Principio di Kruskal" dal nome del suo inventore, Martin David Kruskal (1925-2006).

Pubblicato per la prima volta nel 1975 da Karl Fulves e Martin Gardner(1), il principio è stato analizzato in dettaglio in un articolo scientifico del 2001, scritto da J. C. Lagarias, E. Rains e R. J. Vanderbei(2).

Come altri effetti simili (vedi qui, ad esempio), non è matematicamente certo che funzioni. Scelte nel modo giusto, le condizioni alla base del gioco consentono di presentarlo in una versione che raggiunge la probabilità del 94% di riuscita.

Dal punto di vista statistico, infatti, si rileva che - qualunque sia la carta da cui partire scelta tra le prime dieci - molto spesso la carta finale coincide con quella che si raggiunge partendo dalla prima carta del mazzo. Per il mago è quindi sufficiente eseguire mentalmente i salti dalla prima carta del mazzo a quella finale, effettuando gli opportuni salti indicati, e scrivere - come previsione - il valore della carta su cui si conclude il percorso. Con ogni probabilità, qualunque delle dieci prime carte sceglierà lo spettatore lo condurrà sulla carta prevista.

Qui sotto un esempio di percorso che il mago può effettuare mentalmente:

Dal 4 di quadri si va alla quarta carta successiva, che è un 4 di picche; da questa si va alla quarta carta successiva, che è una donna di picche. Trattandosi di una figura (che quindi vale 1), si va alla carta subito successiva, che è un 2 di cuori. Da questo si salta alla seconda carta a destra, che è un re di quadri, e così via, per arrivare infine al 7 di picche. Trattandosi della 48ma carta, ci fermiamo qui: sarebbe impossibile proseguire oltre la 52ma.

Il mago scrive quindi su un foglietto "Sette di picche": con ogni probabilità, partendo da una qualsiasi delle prime dieci carte, lo spettatore finirà la conta proprio sul sette di picche.

Ciò avverrà spesso, ma... quanto spesso? In altre parole, qual è la probabilità che la previsione sia giusta?

Le probabilità sono state calcolate con una simulazione di Montecarlo che ha preso in considerazione 5000 diversi mazzi di carte.

Poiché è possibile cambiare le condizioni di partenza, sono state valutate situazioni differenti. Le varianti analizzate hanno preso in considerazione:

a) il numero di carte nel mazzo iniziale;

b) il valore dato alle figure (Fante, Donna e Re);

c) l'ampiezza dell'insieme di carte da cui può scegliere di partire lo spettatore;

d) la posizione della carta da cui parte il mago per fare la previsione.

Si è quindi riscontrato che:

- il mazzo di 40 carte è il peggiore che si possa usare: utilizzando i quattro semi delle carte fino al 10 (quindi escludendo le figure), le probabilità di successo sono del 77% circa (colonna rossa); utilizzando invece tutte le 52 carte (e facendo valere 1 le figure) le probabilità sono del 94% circa (colonna verde). In figura sono illustrate le probabilità al variare del numero di carte utilizzate. Come si spiega il salto tra la penultima e l'ultima colonna?

- il salto si spiega con il fatto che le probabilità aumentano all'allungarsi del percorso dalla prima carta scelta all'ultima. Se in un mazzo ci sono tante carte di alto valore, i salti più lunghi riducono il numero di carte che vengono toccate durante il percorso, e questo abbassa le probabilità di successo. Assegnando alle figure il valore 1, si massimizza la lunghezza dei percorsi, migliorando le prestazioni del mazzo. In figura sono illustrate le probabilità di un mazzo di 52 carte al variare dei valori assegnati alle figure. Come si vede, il valore migliore è 1:

- lo spettatore può scegliere di partire da una delle prime 10 carte. Maggiore è l'ampiezza di scelta che gli viene data, minori sono le probabilità che l'effetto si chiuda con successo. Ovviamente, se lo spettatore è costretto a partire dalla prima carta, il gioco funziona il 100% delle volte. E' necessario trovare un giusto equilibrio che faccia percepire allo spettatore una piena libertà ma che contemporaneamente non estenda a tutto il mazzo la possibilità di iniziare la conta. Il valore 10, scelto all'inizio, è del tutto arbitrario e garantisce la già citata probabilità del 94%. Se lo spettatore potesse scegliere di partire da una qualsiasi delle 52 carte, la probabilità sarebbe del 72% circa. In realtà si tratta di un caso limite, impossibile da presentare: c'è, infatti, il rischio che la carta da cui desidera partire lo spettatore sia successiva alla carta prevista, il che abbassa ulteriormente la percentuale stimata. Il 72% non tiene, infatti, conto di questa eventualità. Può essere utile rilevare che il gioco riesce ancora nel 90% dei casi se allo spettatore è concesso di scegliere una delle prime 20 carte, scende invece all'80% se la scelta è allargata alle prime 43 carte. Ecco come varia la probabilità all'aumentare dell'ampiezza della scelta iniziale:

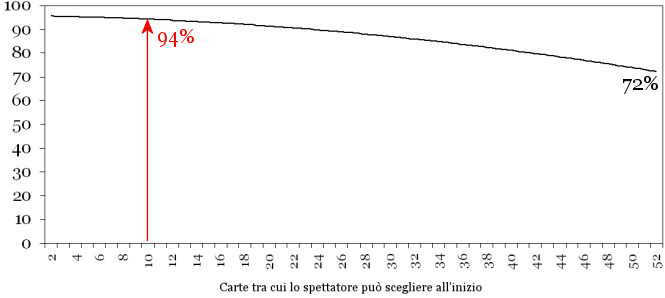
- il fatto che il mago non parta dalla prima carta ma dalla seconda, dalla terza, ecc. ha una lieve influenza sulla percentuale di riuscita, che diminuisce all'aumentare della posizione della carta da cui parte. Ciò è dovuto al fatto che, allontanandosi dalla prima posizione, il percorso in media si accorcia e quindi - da quanto visto sopra - con esso diminuiscono le probabilità di successo. La prima posizione è quindi quella ottimale.

E' possibile provare comodamente una versione virtuale del gioco a questo indirizzo web. Il computer fa la previsione e cliccando sulle varie carte le si scopre, verificando se il computer è stato in grado di prevedere la carta finale.

E' liberamente scaricabile l'algoritmo che ho creato per effettuare l'analisi statistica.

Il principio applicato ai testi

Martin Gardner ha esteso l'idea ai testi(3): supponiamo di avere a disposizione un brano e di poter scegliere una delle prime 10 parole. La lunghezza di ogni parola indicherà a quale parola successiva saltare, come con il mazzo di carte.

Si vede facilmente che l'incipit della Divina Commedia non è un buon testo:

Nel mezzo del cammin di nostra vita mi ritrovai per una selva oscura ché la diritta via era smarrita.

Partendo dalla prima parola, infatti, si potrebbe prevedere di finire su SMARRITA (seguendo il percorso NEL / CAMMIN / PER / OSCURA / SMARRITA).

Se lo spettatore partisse dalla seconda parola, ovvero MEZZO, il percorso si chiuderebbe su VIA: MEZZO / VITA / UNA / CHE / VIA.

L'incipit dei Promessi sposi, invece, consente di presentare il gioco praticamente senza rischi: se lo spettatore sceglie una delle parole in corsivo, finirà invarabilmente su ALTRA.

Quel ramo del lago di Como, che volge a mezzogiorno, tra due catene non interrotte di monti, tutto a seni e a golfi, a seconda dello sporgere e del rientrare di quelli, vien, quasi a un tratto, a ristringersi, e a prender corso e figura di fiume, tra un promontorio a destra, e un'ampia costiera dall'ALTRA parte.

La certezza che funzioni è basata sul fatto che, a differenza del mazzo di carte che può essere mescolato, il brano è fisso e così il numero di lettere che compone le parole nell'ordine in cui compaiono.(4)

_________________

⁽¹⁾ Karl Fulves e Martin Gardner, "The Kruskal Principle" in The Pallbearers Review, giugno 1975

⁽²⁾ http://arxiv.org/PS_cache/math/pdf/0110/0110143v1.pdf

⁽³⁾ Martin Gardner, "Some Math Magic Tricks with Numbers" in Games Magazine, maggio 1999

⁽⁴⁾ Ringrazio Beppe Lo Verso per avermi proposto questo tema.

Questo post è stato pubblicato da Mariano Tomatis il 14 marzo 2010 nella categoria PRECOGNIZIONE

13 marzo 2010

Tricki: riflessioni sul progetto Wiki proposto da Timothy Gowers

Nel corso dell'edizione 2009 del Festival della Matematica di Roma il matematico inglese Timothy Gowers ha presentato una interessante lectio magistralis che può ispirare anche la ricerca illusionistica.

Intitolato "L'effetto a lungo termine di Internet nella ricerca matematica", il suo intervento si riferiva specificamente all'ambito matematico, ma in quasi tutta la sua estensione si sarebbe potuto applicare all'illusionismo e alla magia.

La sua riflessione parte dall'assunto per cui diversi matematici, in luoghi diversi del mondo, si trovano a risolvere problemi simili, con una poco efficiente moltiplicazione di forze individuali, che hanno enormi difficoltà a collaborare aiutandosi vicendevolmente. Ciò non è dovuto ad un intrinseco egoismo da parte dei matematici, quanto più alla mancanza di un coordinamento e di un "luogo" dove le varie soluzioni via via trovate possano essere condivise e messe a disposizione di chi sta risolvendo lo stesso problema. E' chiaro che se due matematici che non si conoscono trascorrono entrambi un mese per risolvere il problema A, senza sapere l'uno dell'altro e ignorando che, un mese prima, qualcuno l'ha già risolto, la matematica progredisce con enorme lentezza.

Quello che Gowers propone è di creare un sito Web accessibile da tutti i matematici, cui tutti possano contribuire dal proprio computer, che contenga una sorta di "Bag of Tricks", una "raccolta di trucchi" utili per risolvere i problemi più vari. Via via che la "borsa" si riempie, i matematici possono disporre di un sempre più ampio campionario di idee da applicare ai propri problemi, e questo può accelerare molto la ricerca, perché ognuno ha a disposizione la conoscenza prodotta dagli altri e può raggiungere velocemente la prima linea, da cui muoversi per fare ricerca su aspetti nuovi e inesplorati.

Il problema di questi "trucchi" sta nel fatto che è difficilissimo catalogarli. Lui fa l'esempio di un indovinello relativo ad alcune strette di mano, che si risolve in un attimo se si conosce il "Principio di Parità", ma che invece richiede ore e ore di analisi se non si conosce lo stesso principio. E' prezioso che il "Principio di parità" venga reso pubblico tra i matematici e messo a disposizione di chi fa ricerca... ma come lo si può catalogare? Se lo metto sotto la lettera P, chi si trova a risolvere il problema delle strette di mano non lo troverà mai, perché non ha nessun motivo di cercare sotto la P qualcosa che risolva il suo problema. La sua proposta è quella di elencare i vari principi e le tecniche scoperte/inventate, per poi scrivere una serie di meta-articoli che riportano dettagliati esempi nei quali i principi stessi possono tornare utili.

L'archivio magico Denis Behr http://archive.denisbehr.de è utile ma inutilizzabile per chi cercasse un modo per contare 7 carte dovendone nascondere 2: se il problema da risolvere è questo, come faccio a sapere dove, in quale libro e chi abbia eventualmente già risolto il mio problema? Sotto quale lettera cerco l'eventuale soluzione?

Gowers ha da poco lanciato il sito "Tricki", che unisce le parole "Trick" e "Wiki": si tratta di un sito prettamente dedicato ai matematici, che sfrutta appieno la potenza di Internet per rendere accessibile a chiunque un vastissimo numero di veri e propri "trucchi" per risolvere problemi. "Tricki" è accessibile all'indirizzo http://www.tricki.org/. Un'ottima introduzione al sito si può trovare sul blog di Gowers, all'indirizzo http://gowers.wordpress.com/2008/10/15/the-forthcoming-launch-of-the-tricki/.

L'estensione all'ambito magico potrebbe essere interessante ma con diverse importanti limitazioni:

1) I "trucchi" dell'arte magica non devono diventare di dominio pubblico: realizzare un sito del genere porrebbe problemi di protezione dell'informazione, che dovrebbe essere accessibile soltanto ad alcuni.

2) A chi dovrebbe essere accessibile uno strumento del genere? Sarebbe forse necessario definire un livello di eccellenza, all'interno del quale si è parte di un gruppo che condivide senza gelosia le proprie idee? E' difficile, oggi, immaginare un organo super partes in grado di fornire una "patente" ai maghi autorizzati ad accedere ad un Tricki dedicato alla magia.

3) Mentre in ambito matematico la paternità delle idee è riconosciuta (perché il primo che fa una scoperta la pubblica su una rivista con data e firma, e da quel momento chiunque citi quell'idea deve fornire il riferimento all'articolo e all'autore originale) in ambito magico i furti di idee senza riconoscere i crediti sono all'ordine del giorno. D'altronde,

4) uno strumento del genere in mano a chi ne fosse fruitore e fornitore responsabile potrebbe ottimizzare gli sforzi di ricerca e fare in modo che ci si occupi di problemi ancora insoluti, piuttosto che di problemi già visti, studiati e superati cento anni fa. Inoltre,

5) un database di questo tipo imporrebbe una analisi molto vasta della stessa "struttura" dei principi alla base della magia, ed afferrandone lo "spirito", molte tecniche uscirebbero dall'ambito del gioco all'interno del quale sono nate per essere applicate a giochi completamente diversi.

Dubito che sia alle porte la possibilità di costituire uno strumento del genere. I problemi 1, 2 e 3 non sono piccoli. Credo che, piuttosto, la provocazione meriti qualche riflessione da parte dei prestigiatori, tanto più che un progetto del genere venne proposto, nel dicembre 2001, da Chris Wasshuber: si intitolava Magic Lineage Project (o Geniiology, dal titolo della celebre rivista Genii), ed è tutt'ora accessibile sul web all'indirizzo http://www.lybrary.com/mlp. Come ha scritto di recente Wasshuber:

Molti anni fa, ben prima che le parole Wiki, Wikipedia e "contributo collettivo" fossero diventate di moda, avevo proposto un approccio "comunitario" all'idea di raccogliere informazioni legate alla magia. La mia proposta non è stata un successo. Né lo sono state più recenti versioni di enciclopedie magiche online. Il problema è che l'illusionismo costituisce una nicchia troppo piccola per attirare un fronte di collaboratori numeroso e sufficiente per far decollare un progetto del genere.

Forse uno strumento cartaceo, una enciclopedia con molteplici riferimenti ipertestuali, potrebbe risolvere il rischio dell'eccessiva diffusione dei segreti stessi, ma che ne sarebbe della necessità di aggiornare continuamente il corpus di conoscenze che un lavoro del genere potrebbe ospitare in cuore? La soluzione non sembra dietro l'angolo.

Questo post è stato pubblicato da Mariano Tomatis il 13 marzo 2010

« POST PIÙ VECCHI

POST PIÙ RECENTI »