16 marzo 2010

Stesso colore al taglio

Prendiamo un mazzo di carte da 40, e "tagliamolo" mettendo la parte sopra sotto; avremo una carta visibile, della quale ci annotiamo il colore.

Adesso "tagliamolo" di nuovo, mettendo la parte sopra sotto; avremo una carta visibile di cui ci annotiamo il colore.

Scommettereste (pre-facto) che i due colori sono uguali?

Non vi conviene: visto che "tagliamo" e non "mescoliamo", la prima carta estratta non può essere la seconda carta estratta, quindi la scelta "stesso colore" ha una possibilità in meno. Le probabilità che le due carte siano dello stesso colore risultano quindi 19/39, meno di 1/2.

Questo problema è tratto dal numero 124 (maggio 2009) della rivista elettronica di giochi matematici Rudi Mathematici: curata da tre geniali autori (che si firmano Rudy d'Alembert, Alice Riddle e Piotr R. Silverbrahms), raccoglie mensilmente una miriade di enigmi, giochi e curiosità matematiche.

Dal primo all'ultimo numero pubblicato, la rivista è disponibile gratuitamente sul sito ufficiale.

Questo post è stato pubblicato da Mariano Tomatis il 16 marzo 2010 nella categoria PRECOGNIZIONE

14 marzo 2010

Il principio di Kruskal

Nel corso di questo articolo approfondirò un principio statistico ingegnoso e molto utile per la cartomagia, chiamato "Principio di Kruskal" dal nome del suo inventore, Martin David Kruskal (1925-2006).

1) Stendi un mazzo di 52 carte faccia in alto, da sinistra verso destra.

2) Scegli una delle prime dieci carte a sinistra. Il suo valore ti indicherà di quante carte a destra spostarti (se ad esempio hai scelto un tre, dovrai spostarti sulla terza carta successiva. Le figure valgono 1).

3) Il valore della nuova carta ti indicherà di quante carte spostarti di nuovo a destra (se ad esempio sei finito su un asso, dovrai spostarti sulla carta successiva).

4) Prosegui gli spostamenti, che verranno indicati ogni volta dal valore della carta scelta, finché arrivi al fondo del mazzo e dalla carta cui sei arrivato non puoi più spostarti senza oltrepassare l'ultima.

Seppure sembri impossibile, il prestigiatore è in grado di prevedere quale sarà la carta finale!

Ciò è reso possibile da un principio statistico ingegnoso e poco noto, chiamato "Principio di Kruskal" dal nome del suo inventore, Martin David Kruskal (1925-2006).

Pubblicato per la prima volta nel 1975 da Karl Fulves e Martin Gardner(1), il principio è stato analizzato in dettaglio in un articolo scientifico del 2001, scritto da J. C. Lagarias, E. Rains e R. J. Vanderbei(2).

Come altri effetti simili (vedi qui, ad esempio), non è matematicamente certo che funzioni. Scelte nel modo giusto, le condizioni alla base del gioco consentono di presentarlo in una versione che raggiunge la probabilità del 94% di riuscita.

Dal punto di vista statistico, infatti, si rileva che - qualunque sia la carta da cui partire scelta tra le prime dieci - molto spesso la carta finale coincide con quella che si raggiunge partendo dalla prima carta del mazzo. Per il mago è quindi sufficiente eseguire mentalmente i salti dalla prima carta del mazzo a quella finale, effettuando gli opportuni salti indicati, e scrivere - come previsione - il valore della carta su cui si conclude il percorso. Con ogni probabilità, qualunque delle dieci prime carte sceglierà lo spettatore lo condurrà sulla carta prevista.

Qui sotto un esempio di percorso che il mago può effettuare mentalmente:

Dal 4 di quadri si va alla quarta carta successiva, che è un 4 di picche; da questa si va alla quarta carta successiva, che è una donna di picche. Trattandosi di una figura (che quindi vale 1), si va alla carta subito successiva, che è un 2 di cuori. Da questo si salta alla seconda carta a destra, che è un re di quadri, e così via, per arrivare infine al 7 di picche. Trattandosi della 48ma carta, ci fermiamo qui: sarebbe impossibile proseguire oltre la 52ma.

Il mago scrive quindi su un foglietto "Sette di picche": con ogni probabilità, partendo da una qualsiasi delle prime dieci carte, lo spettatore finirà la conta proprio sul sette di picche.

Ciò avverrà spesso, ma... quanto spesso? In altre parole, qual è la probabilità che la previsione sia giusta?

Le probabilità sono state calcolate con una simulazione di Montecarlo che ha preso in considerazione 5000 diversi mazzi di carte.

Poiché è possibile cambiare le condizioni di partenza, sono state valutate situazioni differenti. Le varianti analizzate hanno preso in considerazione:

a) il numero di carte nel mazzo iniziale;

b) il valore dato alle figure (Fante, Donna e Re);

c) l'ampiezza dell'insieme di carte da cui può scegliere di partire lo spettatore;

d) la posizione della carta da cui parte il mago per fare la previsione.

Si è quindi riscontrato che:

- il mazzo di 40 carte è il peggiore che si possa usare: utilizzando i quattro semi delle carte fino al 10 (quindi escludendo le figure), le probabilità di successo sono del 77% circa (colonna rossa); utilizzando invece tutte le 52 carte (e facendo valere 1 le figure) le probabilità sono del 94% circa (colonna verde). In figura sono illustrate le probabilità al variare del numero di carte utilizzate. Come si spiega il salto tra la penultima e l'ultima colonna?

- il salto si spiega con il fatto che le probabilità aumentano all'allungarsi del percorso dalla prima carta scelta all'ultima. Se in un mazzo ci sono tante carte di alto valore, i salti più lunghi riducono il numero di carte che vengono toccate durante il percorso, e questo abbassa le probabilità di successo. Assegnando alle figure il valore 1, si massimizza la lunghezza dei percorsi, migliorando le prestazioni del mazzo. In figura sono illustrate le probabilità di un mazzo di 52 carte al variare dei valori assegnati alle figure. Come si vede, il valore migliore è 1:

- lo spettatore può scegliere di partire da una delle prime 10 carte. Maggiore è l'ampiezza di scelta che gli viene data, minori sono le probabilità che l'effetto si chiuda con successo. Ovviamente, se lo spettatore è costretto a partire dalla prima carta, il gioco funziona il 100% delle volte. E' necessario trovare un giusto equilibrio che faccia percepire allo spettatore una piena libertà ma che contemporaneamente non estenda a tutto il mazzo la possibilità di iniziare la conta. Il valore 10, scelto all'inizio, è del tutto arbitrario e garantisce la già citata probabilità del 94%. Se lo spettatore potesse scegliere di partire da una qualsiasi delle 52 carte, la probabilità sarebbe del 72% circa. In realtà si tratta di un caso limite, impossibile da presentare: c'è, infatti, il rischio che la carta da cui desidera partire lo spettatore sia successiva alla carta prevista, il che abbassa ulteriormente la percentuale stimata. Il 72% non tiene, infatti, conto di questa eventualità. Può essere utile rilevare che il gioco riesce ancora nel 90% dei casi se allo spettatore è concesso di scegliere una delle prime 20 carte, scende invece all'80% se la scelta è allargata alle prime 43 carte. Ecco come varia la probabilità all'aumentare dell'ampiezza della scelta iniziale:

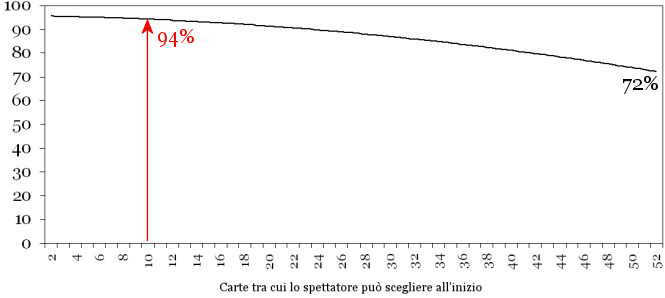
- il fatto che il mago non parta dalla prima carta ma dalla seconda, dalla terza, ecc. ha una lieve influenza sulla percentuale di riuscita, che diminuisce all'aumentare della posizione della carta da cui parte. Ciò è dovuto al fatto che, allontanandosi dalla prima posizione, il percorso in media si accorcia e quindi - da quanto visto sopra - con esso diminuiscono le probabilità di successo. La prima posizione è quindi quella ottimale.

E' possibile provare comodamente una versione virtuale del gioco a questo indirizzo web. Il computer fa la previsione e cliccando sulle varie carte le si scopre, verificando se il computer è stato in grado di prevedere la carta finale.

E' liberamente scaricabile l'algoritmo che ho creato per effettuare l'analisi statistica.

Il principio applicato ai testi

Martin Gardner ha esteso l'idea ai testi(3): supponiamo di avere a disposizione un brano e di poter scegliere una delle prime 10 parole. La lunghezza di ogni parola indicherà a quale parola successiva saltare, come con il mazzo di carte.

Si vede facilmente che l'incipit della Divina Commedia non è un buon testo:

Nel mezzo del cammin di nostra vita mi ritrovai per una selva oscura ché la diritta via era smarrita.

Partendo dalla prima parola, infatti, si potrebbe prevedere di finire su SMARRITA (seguendo il percorso NEL / CAMMIN / PER / OSCURA / SMARRITA).

Se lo spettatore partisse dalla seconda parola, ovvero MEZZO, il percorso si chiuderebbe su VIA: MEZZO / VITA / UNA / CHE / VIA.

L'incipit dei Promessi sposi, invece, consente di presentare il gioco praticamente senza rischi: se lo spettatore sceglie una delle parole in corsivo, finirà invarabilmente su ALTRA.

Quel ramo del lago di Como, che volge a mezzogiorno, tra due catene non interrotte di monti, tutto a seni e a golfi, a seconda dello sporgere e del rientrare di quelli, vien, quasi a un tratto, a ristringersi, e a prender corso e figura di fiume, tra un promontorio a destra, e un'ampia costiera dall'ALTRA parte.

La certezza che funzioni è basata sul fatto che, a differenza del mazzo di carte che può essere mescolato, il brano è fisso e così il numero di lettere che compone le parole nell'ordine in cui compaiono.(4)

_________________

⁽¹⁾ Karl Fulves e Martin Gardner, "The Kruskal Principle" in The Pallbearers Review, giugno 1975

⁽²⁾ http://arxiv.org/PS_cache/math/pdf/0110/0110143v1.pdf

⁽³⁾ Martin Gardner, "Some Math Magic Tricks with Numbers" in Games Magazine, maggio 1999

⁽⁴⁾ Ringrazio Beppe Lo Verso per avermi proposto questo tema.

Questo post è stato pubblicato da Mariano Tomatis il 14 marzo 2010 nella categoria PRECOGNIZIONE

POST PIÙ RECENTI »