La matematica dei cerchi nel grano presenta un aspetto totalmente magico. Semplicissimi compiti svolti ripetutamente possono dare vita a formazioni che incorporano rapporti matematici straordinariamente complessi ed affascinanti. Proviamo a tracciare insieme una formazione, seguendo stupidamente una serie di regole senza porci troppe domande sul risultato finale. Alla fine, osservando il risultato, ci stupiremo nello scoprire quante “cose” sono emerse nel nostro disegno.

Se non è la stagione del grano, o semplicemente non troviamo un contadino che ci autorizzi a piegare parte del suo raccolto, possiamo provarci in un cortile con della ghiaia, su una spiaggia oppure – più modestamente – su un foglio di carta. L’esperimento funziona allo stesso modo se lo proviamo su un bloc-notes o se, come fece il Team Satan, tracciamo un cerchio di quasi 90 metri di diametro su un campo di grano. Ecco le semplici operazioni da eseguire con un compasso e un righello (oppure con una corda e uno stomper).

Prima fase

1) Tracciate un cerchio qualsiasi. Chiameremo C il suo centro (figura a sinistra).

2) Aprite il compasso in modo che una punta tocchi il punto più basso dell’ultimo cerchio tracciato, l’altra il punto più a destra (figura al centro). Con la stessa apertura, tracciate un altro cerchio (più grande del primo) intorno al centro C (figura a destra).

3) Ripetete il punto 2 più volte, e fermatevi soltanto quando siete stufi.

Irving, Lundberg e Dickinson erano partiti da un cerchio di 7 metri abbondanti, e dopo aver ripetuto il punto 2 per cinque volte, avevano superato i 40 metri. Voi potete fermarvi quando volete: come regola generale, cercate di non uscire dai bordi della pagina (o di non uscire dai confini del campo). Supponiamo che vi fermiate dopo aver tracciato cinque cerchi:

Di fronte a voi ci sono una serie di cerchi concentrici. Immaginate che si tratti di una torta da dividere tra 16 persone: cercate di tagliarla a spicchi tutti uguali. Se lavorerete su un campo di grano, la cosa sarà appena più difficile: il Teorema del Coseno (1)  potrà tornarvi molto utile, oppure potrete fare una serie di fare bisezioni ripetute come fareste con riga e compasso. Su un foglio di carta, sarà facile come affettare una pizza. Colorate quindi il cerchio più interno (o, se siete su un campo, abbattete tutto il grano che circonda).

Siete pronti per la seconda e ultima fase.

Seconda fase

1) Scegliere uno spicchio qualsiasi. Partendo dal cerchio più esterno, muovetevi a zig-zag all’interno dello stesso spicchio per raggiungere il cerchio successivo, poi il successivo, fino ad arrivare a quello centrale. Ripetete due volte la procedura, intrecciando il primo percorso con un secondo speculare.

2) Ripetete il punto 1 per tutti i sedici spicchi.

La figura cui arriviamo è qui illustrata:

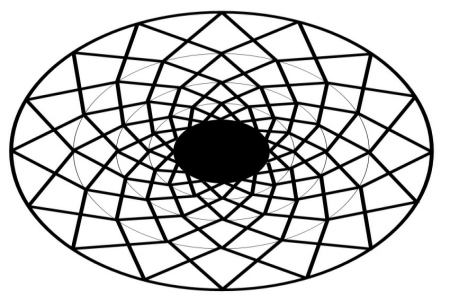
Senza accorgercene, abbiamo creato un’immagine densa di simbolismo esoterico.

La prima fase di costruzione faceva in modo che ogni cerchio più grande avesse un raggio pari al lato del quadrato inscritto nel cerchio più piccolo. Questa procedura, eseguita da noi meccanicamente, senza eccessive preoccupazioni simboliche, assume per i “credenti” nel fenomeno dei cerchi nel grano dei profondi significati alchemici. Ecco come la descrive Bert Janssen, uno studioso di simbologia dei crop circles:

Molte formazioni hanno mostrato connessioni più o meno nascoste con l’Alchimia e in particolare con l’interazione tra lo Spirito e la Materia. [...] Cominciamo da un quadrato inscritto in un cerchio. Lo Spirito (la sfera) che circonda la Materia (il cubo). Un nuovo quadrato circonderà il cerchio e un secondo cerchio circonderà il secondo quadrato. Possiamo ripetere questa procedura più volte, generando una serie di cerchi e quadrati. Strati alternati di Spirito e Materia.

Sapevate di realizzare qualcosa di così altamente simbolico? Probabilmente no: pensavate probabilmente a tutt’altro durante i passi ripetuti della prima fase di costruzione. Eppure, il frutto del vostro lavoro incarna l’essenza stessa della magia; come scrive Janssen:

La formazione mostra l’annidamento di cerchi e quadrati a partire da un grande cerchio all’interno del quale si ripetono cerchi sempre più piccoli. Ciò che è nel grande è come ciò che è nel piccolo. Ciò che è in alto è come ciò che è in basso.

Ma passiamo alla seconda fase, a vostra insaputa ancora più fertile di significati magici. I vari percorsi a zig-zag, realizzati pedestremente seguendo sempre la stessa regola, hanno prodotto una serie di spirali molto particolari, che si intrecciano in senso orario e antiorario e che i matematici chiamano “spirali logaritmiche di Fibonacci”. Si tratta di figure molto affascinanti non solo dal punto di vista estetico: hanno infatti molte proprietà matematiche particolari, talmente complesse che sembra impossibili poterle realizzare di notte al buio in un campo di grano o su un foglio di carta senza far uso di calcoli complessi. Per accorgerci di quanto l’immagine appaia complicata, dobbiamo mostrarla a qualcuno che non ha seguito la procedura di costruzione: difficilmente costui si accorgerà che non è che la stupida ripetizione di tante righe a zig-zag, che collegano punti ottenuti tracciando un cerchio dentro l’altro. Potrebbe quindi ricordarvi che simili spirali orarie e antiorarie si intrecciano al centro dell’infiorescenza dei girasoli, e il rapporto tra il numero di tali spirali tende al numero phi (che i matematici chiamano anche “sezione aurea”), trattandosi del rapporto tra due numeri di Fibonacci sempre più grandi a seconda delle dimensioni del fiore. Qualche ricercatore della fazione dei “credenti” arriva a riconoscervi addirittura un messaggio per l’evoluzione dell’intera umanità. Meditate con attenzione le terribili parole di Adriano Forgione che descrivono il vostro cerchio:

Se l’uomo è destinato a tornare al cosmo, come avverrà tutto ciò? I crops sembrano ancora una volta contenere la risposta ed è ancora la spirale a indicarci la strada. […] Infatti la spirale aurea è basata sul valore di 1,615 che è un numero ricorrente in natura, riscontrato nel fiore di girasole così come nella spirale delle galassie. È inoltre presente nella doppia elica del DNA. La sequenza numerica di Fibonacci, così concepita, basilare per la geometria sacra delle civiltà antiche, è la chiave per capire come la natura disegni le sue creature (alberi, fiori, ecc.). È inoltre uno dei fondamenti della fisica convenzionale. È quanto stiamo scoprendo oggi, accettando il fatto che l’Universo abbia più dimensioni o passaggi intercomunicanti nei quali i nostri visitatori viaggiano senza problemi, utilizzando delle feritoie in una griglia interdimensionale che si dischiude esattamente come una spirale.

Supponiamo che vi troviate in tribunale e veniate accusati di aver realizzato il vostro cerchio con l’intento di nascondervi riferimenti allo Spirito e alla Materia, all’elica del DNA, ai passaggi galattici interdimensionali e alla sequenza di Fibonacci. Al giudice potreste rispondere: «Mi creda, io ho seguito poche stupide regole che ho trovato su un libro: non avevo idea di che cosa stavo facendo, né intendevo minimamente realizzare quello che mi accusate di aver creato.» Occultamento colposo di simboli esoterici? L’unica vostra speranza è che il giudice si fidi delle vostre originali intenzioni, perché se dovesse giudicarvi per il risultato, sareste costretti ad ammettere che da poche e semplici regole è emerso magicamente qualcosa di complesso ed evocativo. Si tratta di un fenomeno ben noto in ambito matematico, in particolare nella teoria del caos, ed è qualcosa che i circlemaker sono abilissimi a sfruttare per semplificare al massimo il loro lavoro pur realizzando opere che vengono ritenute troppo complicate per avere un’origine umana.

Quello della “complessità emergente” è il trucco meglio custodito di questa branca dell’illusionismo. Rob Irving e John Lundberg descrivono così l’opera che abbiamo appena completato:

L’ispirazione ci venne dai dipinti di illusioni ottiche note come Op Art, create da artisti come Bridget Riley e Victor Varsley. Questi artisti utilizzavano le illusioni ottiche per realizzare dipinti in grado di far vibrare la retina e sfidare il cervello ad interpretare le immagini mentre queste sembravano muoversi e modificarsi in modi strani e apparentemente impossibili. Queste forme sono l’ideale per i circlemaker che vogliano ottenere effetti che sembrino impossibili da realizzare, spingendo più in là i limiti di ciò che è considerato umanamente possibile in questo ambito. […] La chiave di un cerchio nel grano di successo è una certa complessità visuale basata su semplici e ripetitivi elementi geometrici. […] Le curve [delle spirali] sono composte da piccoli segmenti tutti uguali, che si intrecciano all’interno di ognuno degli spicchi della formazione. Seppure appaiano particolarmente complesse, in realtà sono molto semplici da costruire, e poiché gli elementi all’interno di ogni settore sono tutti identici, la costruzione può avvenire molto velocemente.

Se la matematica ci mette lo zampino, facendo saltar fuori la sezione aurea senza che l’avessimo preventivata, il resto ce lo mette l’immaginazione umana: basta rileggere i testi di Janssen e di Forgione per accorgersi di quante delle interpretazioni suggerite abbiano a che fare con la loro fantasia piuttosto che con un messaggio che ci arriva dallo spazio.

Bibliografia

Questo articolo è tratto dal mio libro La magia dei numeri, Milano, Kowalski, 2010.

Il più grande studioso di crop circle del mondo è italiano: si chiama Francesco Grassi, ha pubblicato un articolo scientifico sul Journal of Scientific Exploration (Vol. 19, n.2, pp. 159-170, 2005) e cura un fantastico blog sull’argomento.

Note