A magical book of the 16th century (discover it here) can be used as a tool for funny mathematical puzzles. The letters on the tables of the “Book of Soyga” are not distributed at random, and a study of their regularities may reveal curious details and does not require knowledge of higher mathematics.

A first interesting question may be: Is it possible to create words of sense within the table by adjusting the “magic word”?

Let us reflect on the first row.

The first row

The mathematical rule to compile the first row can be condensed in this graph:

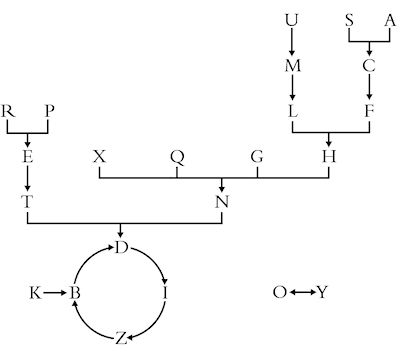
The rule that determines the sequence of letters on the first row of a Soyga table.

Since an arrow leads from U to M, in the first row of a Sogya table on the right of every U a M will appear. Iteratively, as an arrow connects the M and L, L will always appear to the right of M. Freely set the first letter on the left, and all subsequent will be determined by the rule.

The first table begins with the letter N. Following the arrow, the next letter is D. At this point, the path is closed in a circle that touches in succession the letters D/I/Z/B. So the first row of the first table will contain an N followed by the letters DIZB, cyclically repeated.

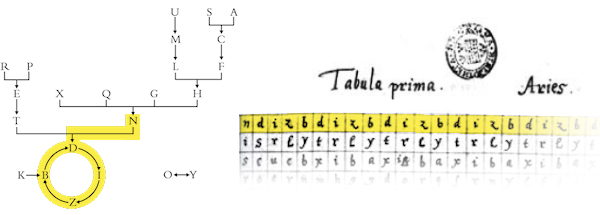
Highlighted in yellow the path that leads to the definition of the first row of the first table of Soyga.

Looking at the graph of the rule we note that any point leads to the fateful cycle – with the exception of the letters O and Y: these two create a smaller cycle (it happens, for example, on the fifth Soyga table, whose first letter is an O).

In chaos theory, the sequences DIZB and OY would be called “attractors” (1) , because they seem to “attract” the paths as would a black hole – which is why Michael W. Ecker prefers to call them “mathemagical black holes” (2) .

The existence of these two attractors makes impractical the idea of selecting properly the first letter to make a word of sense on the first row; in just a few steps, a path starting from any letter collapses into the sequence DIZBDIZBDIZB…

A more promising field of play is the second column of the table.

The second column

Suppose I want to write the word DIAMOND on the second column. To “produce” the D, the rule that defines the first row suggests that I use N as a seed. (3) 

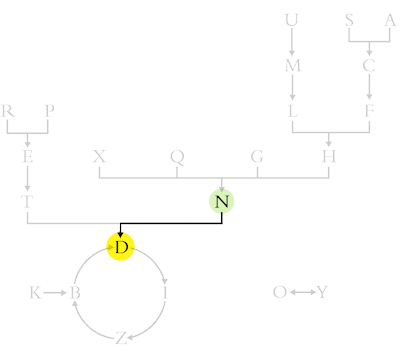
The N, in fact, is always followed by D.

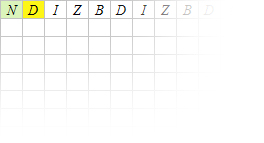
Under the D, I need an I. What letter should I put on the left which – crossed with the D – “produce” an I?

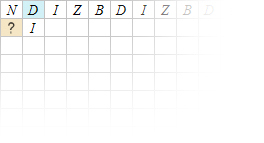
The rule presented above applies only on the first line; whoever compiled the tables of the “Book of Soyga” probably used a double wheel of Ramon Llull (1235-1316) like this:

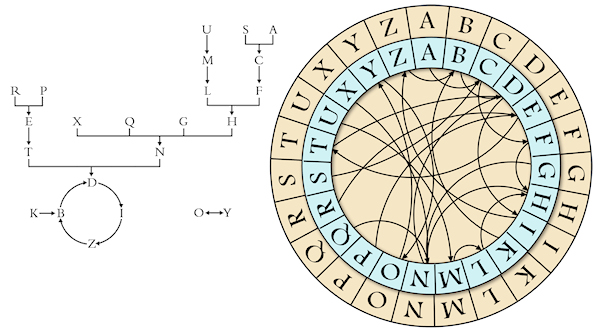
The same arrows appearing on the left graph are reproduced on the right, but since the blue crown-wheel can rotate, the tool can be used to “compute” easily the letters of all rows.

If I have an F in the left and an L over, which letter I shall write in the square with the black border? By rotating the central crown so that L coincides with the external F, I get this arrangement:

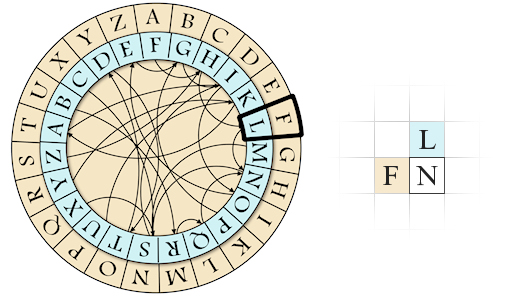
Since the arrow from the L ends on N, this is the letter we write in the square.

As a computer ante litteram, the wheels of Llull represented here allow to quickly determine all the letters of a Soyga table!

The instrument can be used to solve my problem: What letter should I put on the left which – crossed with the D – “produce” an I? The technique is to turn the crown until, in the fixed background, a arrow linking D to I appears. The rotation is the one that aligns the D and H – so the latter must be the second letter of the seed:

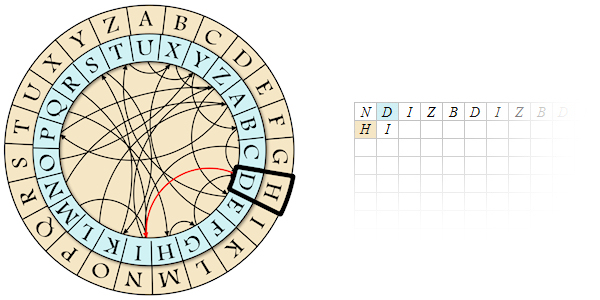
Continuing in this way, I can produce the whole word DIAMOND from the obscure “magic word” NHXRFMN:

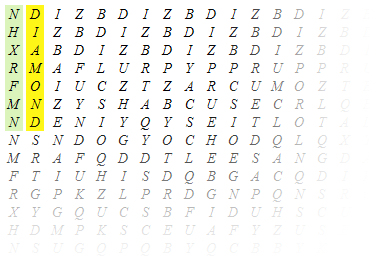
Click here to see the complete table.

If you want to start playing, an interesting challenge is to find the seeds that produce the following words (click on each to access the corresponding table, which shows the solution on the first column): BAGFUL BRONCO BYEBYE CENSURE CENSURED CENSURES CLAMOUR CLAMOURED CONSUL CONSULT CONSULTS CONTAGION COUCHED COUCHES COURTLY COURTS CRESCENT CRESCENTS CROFTS CRONES CROUCH CROUCHED CROUCHES DIAMOND DIAMONDS DIRELY DIRTILY DRENCH DRENCHED DRENCHES DRIFTS DRONED DRONES ENAMOURED ENSCONCE ENSCONCED ENSUED ENSUES ENSURE ENSURED ENSURES ENTAIL ENTIRE ENTIRELY ENTIRES EUREKA FENCED FENCES FRENCH FRESCO FRESHEN FRESHENED FRESHENS FRONDS FRONTS IRONED LACHES LAMBDA LAPFUL LYNCHED LYNCHES MONACO MOTION MOTIONED MOTIONS MOULTS MULCHES NEURON NEURONE NEURONES NEURONS ODIUMS OUTBRED OUTSHONE OUTSIZE OUTSKIRTS TACHYON TACHYONS YACHTS

Looking for the longest word that can be produced is more difficult; the longest I’ve found so far is CONCRETIONS (11 letters). In Italian, CONCEDIAMOLA is 12 letters long.

Can you find a longer word?

Notes