Essential Magic Conference logo is a trip-let, a 3-dimensional object shaped in such a way that its projections along three mutually perpendicular axes are three different letters of the alphabet.

The first trip-let in print was Douglas R. Hofstadter’s “GEB” which is illustrated on the cover of his Gödel, Escher, Bach: it is a visual summary of the book, dealing with the intrinsic unity of Kurt Gödel’s, Mauritius C. Escher’s and Johann S. Bach’s works.

In Hofstadter’s words,

The trip-let idea came to me in a flash one evening as I was trying to think how best to symbolize the unity of Gödel, Escher, and Bach by somehow fusing their names in a striking design. The two trip-lets shown on the cover were designed and made by me, using mainly a band saw, with an end mill for the holes; they are redwood, and are just under 4 inches on a side. (1) 

Two trip-lets by Douglas R. Hofstadter (1979)

Designing trip-lets

Designing trip-lets is not a trivial work, and with some combinations of letters it is impossible to create a single object producing three correct projections.

Let’s create a homage for Marco Tempest, Luis De Matos and David Britland – the three minds behind the EMC: our purpose is to design a MLD trip-let.

Zach Hoeken, whose

true passion in life is acting as a catalyst and helping others do amazing things [and] create an awesome world to live in. (2) 

provides in his website a wonderfully simple OpenSCAD script (download it from here) with the geometrical structure of all the 26 letters.

The .scad script should be opened in a text editor and the last function modified as follows:

TripLet(5, 12, 4, 0, 0, 0, 0);

where each of the first three numbers correspond to a letter. 12 corresponds to L, the 12th letter. 4 corresponds to D. For the letter M, I used the number 5 correspondong to E to better mimic the original EMC logo, considering that M can be obtained by rotating E by 90 degrees.

The resulting .scad file (download it from here) can easily be compiled with OpenSCAD, a open source software for 3-dimensional rendering. The result is this:

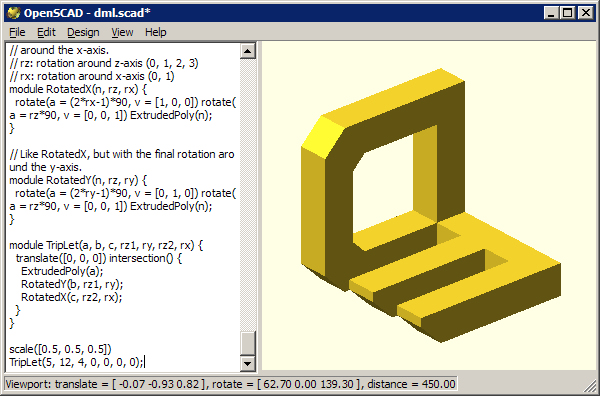
With OpenSCAD you can also export the trip-let in STL format (download it from here), to analyse it with a STL viewer: just put in the textbox the content of the .stl file, click RENDER and... enjoy!

Creating deeper connections by adding a context

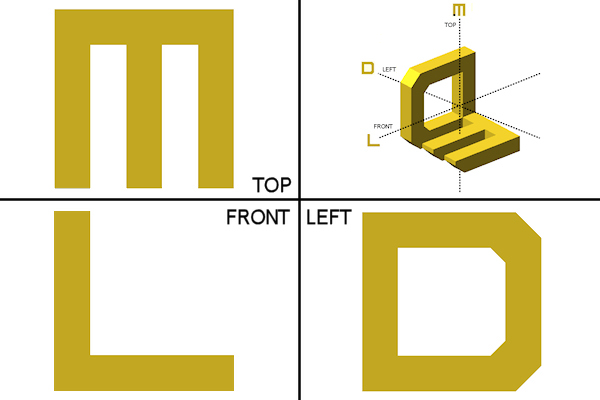
Disclaimer: If you are not a magician or if you didn’t attend the Essential Magic Conference 2011, you’ll find this paragraph extremely esoteric!

The correspondence between the letters and the organizers of Essential Magic Conference is still weak, because so far it is based only on their first names. To create a deeper link it is necessary to put them in a context relating to their personal style in magic, and their speeches were great sources of inspiration for this.

David Britland spoke about Chan Canasta, well known for his psychological card forces. Think of a card, and memorize its letter:

Dai Vernon would bet you have chosen card D... is it correct? Oops!

Luis De Matos (3)  described in detail his method for making a car disappear. What if he had to explain a method one century ago, at the EMC 1911? He probably would have used a big L for his chart:

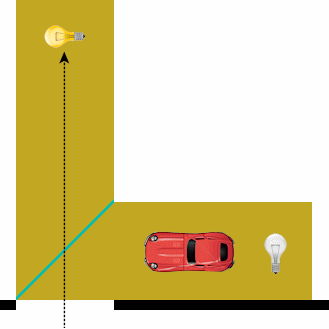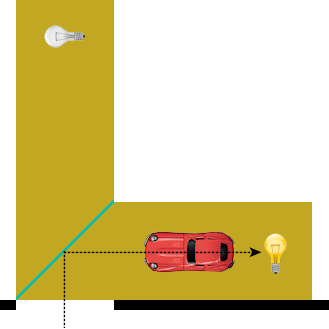
Marco Tempest and his interest in digital technologies are synonimous of electronic devices and YouTube videos. That’s why I took my pocket calculator and shot a video, then uploaded on YouTube, in order to share my discovery. There is a secret message on the EMC website. In the “Learn more in 60 seconds” video there is a suspicious series of numbers. On my pocket calculator, I digited them all without performing any calculation – just separating them with an alternance of M+ and M-.

60 seconds to summarize the EMC? I pressed 60 and M+
33 speakers? I pressed 33 and M-
16 hours of live video? 16 and M+
From 7 to 9 July? 7 and M-, followed by 9 and M+
Max Maven’s lucky number was 42? 42 followed by M-

Each number was a piece of a secret code. I just needed the key to unlock it. Then I discovered it. Marco’s signature was hidden in plain view in front of me. One button was labelled MRC. Marco’s three consonants!

I pressed it, and I got... the digit 3: the only digit which, rotated by 90 degrees, is the letter M.

Trip-lets in the past

In the 17th century Fra Innocenzo da Petralia (1591-1648) carved a crucifix in the wood which now is considered “miraculous”; as if it was a trip-let, the face of Christ shows three different expressions according to different points of view: chronologically, Christ is “suffering”, “dying” and “dead”.

Christ suffering, Christ dying and Christ dead

The effect is due to the structure of eyes and mouth, which from different perspectives seem to close. The difference between the third image and the others is great, but the effect is not so strong when comparing the first two.

In 1788 the crucifix was donated by marquis Carlo Mosca Barzi (1720-1790) to the city of Gradara, a town in the region of Marche in central Italy. Its castle is famous as being the location of the episode of Paolo and Francesca described by Dante Alighieri in the 5th Canto of his Inferno. The crucifix is now in the St. John Church.

Puzzles about Trip-lets – The Cork Plug

Figuring out the shape of a trip-let can be a difficult task. How a cork can be carved to fit snugly into square, circular and triangular holes?

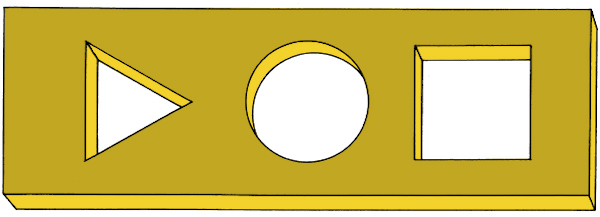
This old puzzle is discussed by Martin Gardner (1914-2010) in his The Second Scientific American Book of Puzzles & Diversions (4) : the solution is a peculiar trip-let involving the most simple geometric shapes (see the 3-dimensional solution here).

Puzzles about Trip-lets – The mysterious shape

Can you discover the left projection of this object with identical top and front projections?

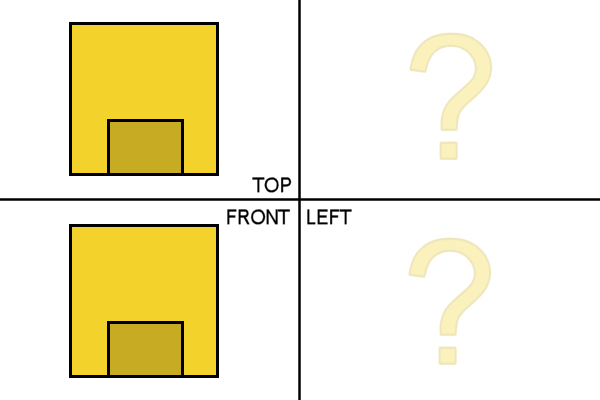
What is its shape? (See here the solution)

Notes